What Is the Equivalent Capacitance of the Circuit to the Right?

Capacitance

50 Capacitors in Serial and in Parallel

Learning Objectives

By the cease of this section, you volition be able to:

Explain how to determine the equivalent capacitance of capacitors in series and in parallel combinations
Compute the potential divergence across the plates and the charge on the plates for a capacitor in a network and determine the net capacitance of a network of capacitors

Several capacitors tin can be connected together to be used in a diversity of applications. Multiple connections of capacitors acquit as a single equivalent capacitor. The total capacitance of this equivalent single capacitor depends both on the individual capacitors and how they are connected. Capacitors can be arranged in 2 simple and common types of connections, known as series and parallel, for which we can easily calculate the full capacitance. These 2 basic combinations, series and parallel, can as well be used equally role of more circuitous connections.

The Series Combination of Capacitors

(Figure) illustrates a series combination of three capacitors, arranged in a row inside the circuit. As for any capacitor, the capacitance of the combination is related to the charge and voltage past using (Figure). When this series combination is connected to a battery with voltage Five, each of the capacitors acquires an identical accuse Q. To explain, first note that the charge on the plate connected to the positive terminal of the battery is $+Q$ and the charge on the plate connected to the negative terminal is $\text{−}Q$ . Charges are and so induced on the other plates then that the sum of the charges on all plates, and the sum of charges on any pair of capacitor plates, is zip. However, the potential drop ${V}_{1}=Q\text{/}{C}_{1}$ on ane capacitor may be unlike from the potential drop ${V}_{2}=Q\text{/}{C}_{2}$ on another capacitor, because, generally, the capacitors may have different capacitances. The serial combination of two or three capacitors resembles a single capacitor with a smaller capacitance. More often than not, any number of capacitors continued in series is equivalent to one capacitor whose capacitance (called the equivalent capacitance) is smaller than the smallest of the capacitances in the series combination. Charge on this equivalent capacitor is the same as the charge on any capacitor in a series combination: That is, all capacitors of a serial combination have the same charge. This occurs due to the conservation of accuse in the circuit. When a charge Q in a series excursion is removed from a plate of the get-go capacitor (which we denote as $\text{−}Q$ ), information technology must be placed on a plate of the second capacitor (which we denote as $+Q\right),$ and so on.

(a) Three capacitors are connected in series. The magnitude of the charge on each plate is Q. (b) The network of capacitors in (a) is equivalent to one capacitor that has a smaller capacitance than any of the individual capacitances in (a), and the accuse on its plates is Q.

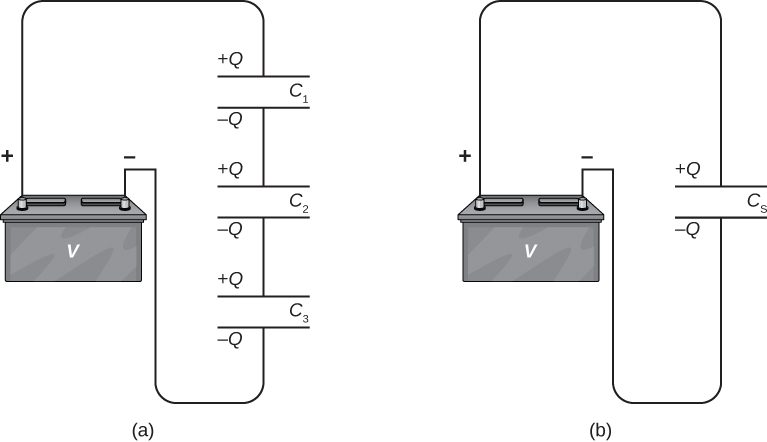
Figure a shows capacitors C1, C2 and C3 in series, connected to a battery. Figure b shows capacitor Cs connected to the battery.

Nosotros can discover an expression for the total (equivalent) capacitance by considering the voltages beyond the private capacitors. The potentials across capacitors one, two, and 3 are, respectively, ${V}_{1}=Q\text{/}{C}_{1}$ , ${V}_{2}=Q\text{/}{C}_{2}$ , and ${V}_{3}=Q\text{/}{C}_{3}$ . These potentials must sum upwardly to the voltage of the bombardment, giving the following potential balance:

$V={V}_{1}+{V}_{2}+{V}_{3}.$

Potential V is measured beyond an equivalent capacitor that holds charge Q and has an equivalent capacitance ${C}_{\text{S}}$ . Entering the expressions for ${V}_{1}$ , ${V}_{2}$ , and ${V}_{3}$ , we get

$\frac{Q}{{C}_{\text{S}}}=\frac{Q}{{C}_{1}}+\frac{Q}{{C}_{2}}+\frac{Q}{{C}_{3}}.$

Canceling the charge Q, nosotros obtain an expression containing the equivalent capacitance, ${C}_{\text{S}}$ , of three capacitors connected in series:

$\frac{1}{{C}_{\text{S}}}=\frac{1}{{C}_{1}}+\frac{1}{{C}_{2}}+\frac{1}{{C}_{3}}.$

This expression tin be generalized to whatsoever number of capacitors in a series network.

Serial Combination

For capacitors connected in a series combination, the reciprocal of the equivalent capacitance is the sum of reciprocals of individual capacitances:

$\frac{1}{{C}_{\text{S}}}=\frac{1}{{C}_{1}}+\frac{1}{{C}_{2}}+\frac{1}{{C}_{3}}+\text{⋯}.$

Equivalent Capacitance of a Serial Network Find the total capacitance for three capacitors continued in series, given their individual capacitances are $1.000\phantom{\rule{0.2em}{0ex}}\mu \text{F}$ , $5.000\phantom{\rule{0.2em}{0ex}}\mu \text{F}$ , and $8.000\phantom{\rule{0.2em}{0ex}}\mu \text{F}$ .

Strategy Considering there are only three capacitors in this network, we can discover the equivalent capacitance past using (Figure) with three terms.

Solution We enter the given capacitances into (Figure):

$\begin{array}{ccc}\hfill \frac{1}{{C}_{\text{S}}}& =\hfill & \frac{1}{{C}_{1}}+\frac{1}{{C}_{2}}+\frac{1}{{C}_{3}}\hfill \\ & =\hfill & \frac{1}{1.000\phantom{\rule{0.2em}{0ex}}\mu \text{F}}+\frac{1}{5.000\phantom{\rule{0.2em}{0ex}}\mu \text{F}}+\frac{1}{8.000\phantom{\rule{0.2em}{0ex}}\mu \text{F}}\hfill \\ \hfill \frac{1}{{C}_{\text{S}}}& =\hfill & \frac{1.325}{\mu \text{F}}.\hfill \end{array}$

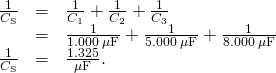
Now we invert this upshot and obtain ${C}_{\text{S}}=\frac{\mu \text{F}}{1.325}=0.755\phantom{\rule{0.2em}{0ex}}\mu \text{F}\text{.}$

Significance Note that in a series network of capacitors, the equivalent capacitance is ever less than the smallest individual capacitance in the network.

The Parallel Combination of Capacitors

A parallel combination of 3 capacitors, with one plate of each capacitor continued to 1 side of the circuit and the other plate connected to the other side, is illustrated in (Figure)(a). Since the capacitors are connected in parallel, they all take the same voltage Five across their plates. Notwithstanding, each capacitor in the parallel network may store a different charge. To find the equivalent capacitance ${C}_{\text{P}}$ of the parallel network, we note that the total charge Q stored past the network is the sum of all the individual charges:

$Q={Q}_{1}+{Q}_{2}+{Q}_{3}.$

On the left-hand side of this equation, we use the relation $Q={C}_{\text{P}}V$ , which holds for the entire network. On the correct-hand side of the equation, we utilize the relations ${Q}_{1}={C}_{1}V,{Q}_{2}={C}_{2}V,$ and ${Q}_{3}={C}_{3}V$ for the iii capacitors in the network. In this way we obtain

${C}_{\text{P}}V={C}_{1}V+{C}_{2}V+{C}_{3}V.$

This equation, when simplified, is the expression for the equivalent capacitance of the parallel network of iii capacitors:

${C}_{\text{P}}={C}_{1}+{C}_{2}+{C}_{3}.$

This expression is easily generalized to whatsoever number of capacitors continued in parallel in the network.

Parallel Combination

For capacitors connected in a parallel combination, the equivalent (net) capacitance is the sum of all individual capacitances in the network,

${C}_{\text{P}}={C}_{1}+{C}_{2}+{C}_{3}+\text{⋯}.$

(a) 3 capacitors are connected in parallel. Each capacitor is connected direct to the battery. (b) The charge on the equivalent capacitor is the sum of the charges on the individual capacitors.

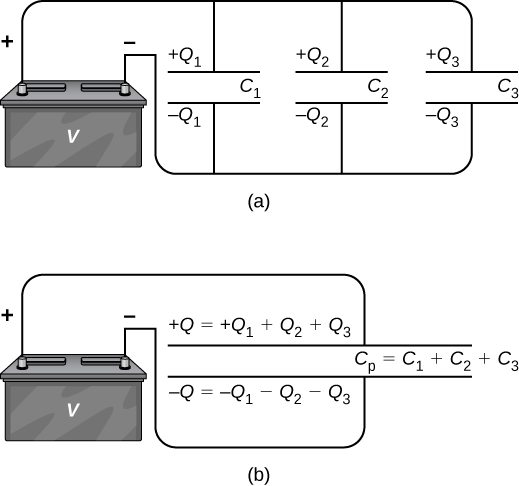
Equivalent Capacitance of a Parallel Network Find the net capacitance for iii capacitors continued in parallel, given their individual capacitances are $1.0\phantom{\rule{0.2em}{0ex}}\mu \text{F},5.0\phantom{\rule{0.2em}{0ex}}\mu \text{F},\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}8.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}\text{.}$

Strategy Because there are simply three capacitors in this network, we tin find the equivalent capacitance by using (Figure) with three terms.

Solution Entering the given capacitances into (Figure) yields

$\begin{array}{ccc}\hfill {C}_{\text{P}}& =\hfill & {C}_{1}+{C}_{2}+{C}_{3}=1.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}+5.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}+8.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}\hfill \\ \hfill {C}_{\text{P}}& =\hfill & 14.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}\text{.}\hfill \end{array}$

Significance Note that in a parallel network of capacitors, the equivalent capacitance is ever larger than any of the individual capacitances in the network.

Capacitor networks are commonly some combination of series and parallel connections, as shown in (Figure). To notice the net capacitance of such combinations, we place parts that contain merely series or only parallel connections, and detect their equivalent capacitances. We echo this process until we can determine the equivalent capacitance of the entire network. The following example illustrates this process.

Equivalent Capacitance of a Network Find the total capacitance of the combination of capacitors shown in (Figure). Presume the capacitances are known to three decimal places $\left({C}_{1}=1.000\phantom{\rule{0.2em}{0ex}}\mu \text{F},{C}_{2}=5.000\phantom{\rule{0.2em}{0ex}}\mu \text{F,}$ ${C}_{3}=8.000\phantom{\rule{0.2em}{0ex}}\mu \text{F}\right)\text{.}$ Round your respond to three decimal places.

Strategy We commencement identify which capacitors are in serial and which are in parallel. Capacitors ${C}_{1}$ and ${C}_{2}$ are in series. Their combination, labeled ${C}_{\text{S}},$ is in parallel with ${C}_{3}.$

Solution Since ${C}_{1}\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}{C}_{2}$ are in series, their equivalent capacitance ${C}_{\text{S}}$ is obtained with (Figure):

$\frac{1}{{C}_{\text{S}}}=\frac{1}{{C}_{1}}+\frac{1}{{C}_{2}}=\frac{1}{1.000\phantom{\rule{0.2em}{0ex}}\mu \text{F}}+\frac{1}{5.000\phantom{\rule{0.2em}{0ex}}\mu \text{F}}=\frac{1.200}{\mu \text{F}}⇒{C}_{\text{S}}=0.833\phantom{\rule{0.2em}{0ex}}\mu \text{F}\text{.}$

Capacitance ${C}_{\text{S}}$ is connected in parallel with the third capacitance ${C}_{3}$ , so we employ (Effigy) to find the equivalent capacitance C of the entire network:

$C={C}_{\text{S}}+{C}_{3}=0.833\phantom{\rule{0.2em}{0ex}}\mu \text{F}+8.000\phantom{\rule{0.2em}{0ex}}\mu \text{F}=8.833\phantom{\rule{0.2em}{0ex}}\mu \text{F}\text{.}$

Network of Capacitors Decide the internet capacitance C of the capacitor combination shown in (Effigy) when the capacitances are ${C}_{1}=12.0\phantom{\rule{0.2em}{0ex}}\mu \text{F},{C}_{2}=2.0\phantom{\rule{0.2em}{0ex}}\mu \text{F},$ and ${C}_{3}=4.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}$ . When a 12.0-5 potential difference is maintained beyond the combination, find the charge and the voltage across each capacitor.

(a) A capacitor combination. (b) An equivalent ii-capacitor combination.

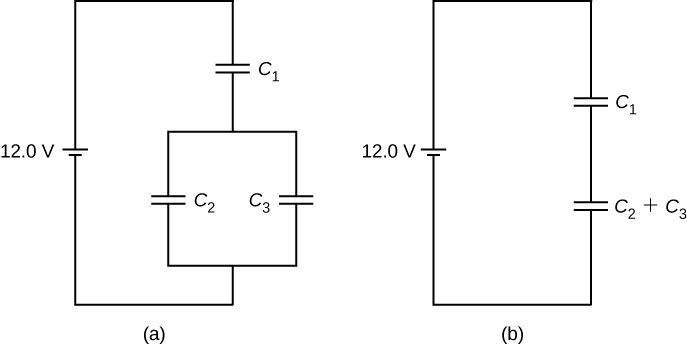
Figure a shows capacitors C1 and C2 in series and C3 in parallel with them. The value of C1 is 1 micro Farad, that of C2 is 5 micro Farad and that of C3 is 8 micro Farad. Figure b is the same as figure a, with C1 and C2 being replaced with equivalent capacitor Cs. Figure c is the same as figure b with Cs and C3 being replaced with equivalent capacitor C tot. C tot is equal to Cs plus C3.

Strategy Nosotros first compute the net capacitance ${C}_{23}$ of the parallel connection ${C}_{2}$ and ${C}_{3}$ . Then C is the internet capacitance of the series connectedness ${C}_{1}$ and ${C}_{23}$ . We utilize the relation $C=Q\text{/}V$ to notice the charges ${Q}_{1}$ , ${Q}_{2}$ , and ${Q}_{3}$ , and the voltages ${V}_{1}$ , ${V}_{2}$ , and ${V}_{3}$ , across capacitors 1, 2, and 3, respectively.

Solution The equivalent capacitance for ${C}_{2}$ and ${C}_{3}$ is

${C}_{23}={C}_{2}+{C}_{3}=2.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}+4.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}=6.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}\text{.}$

The entire three-capacitor combination is equivalent to two capacitors in series,

$\frac{1}{C}=\frac{1}{12.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}}+\frac{1}{6.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}}=\frac{1}{4.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}}⇒C=4.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}\text{.}$

Consider the equivalent two-capacitor combination in (Figure)(b). Since the capacitors are in series, they take the aforementioned charge, ${Q}_{1}={Q}_{23}$ . Also, the capacitors share the 12.0-V potential difference, so

$12.0\phantom{\rule{0.2em}{0ex}}\text{V}={V}_{1}+{V}_{23}=\frac{{Q}_{1}}{{C}_{1}}+\frac{{Q}_{23}}{{C}_{23}}=\frac{{Q}_{1}}{12.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}}+\frac{{Q}_{1}}{6.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}}⇒{Q}_{1}=48.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}.$

Now the potential difference beyond capacitor one is

${V}_{1}=\frac{{Q}_{1}}{{C}_{1}}=\frac{48.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}}{12.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}}=4.0\phantom{\rule{0.2em}{0ex}}\text{V}\text{.}$

Because capacitors 2 and iii are connected in parallel, they are at the aforementioned potential difference:

${V}_{2}={V}_{3}=12.0\phantom{\rule{0.2em}{0ex}}\text{V}-4.0\phantom{\rule{0.2em}{0ex}}\text{V}=8.0\phantom{\rule{0.2em}{0ex}}\text{V}.$

Hence, the charges on these two capacitors are, respectively,

$\begin{array}{l}{Q}_{2}={C}_{2}{V}_{2}=\left(2.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}\right)\left(8.0\phantom{\rule{0.2em}{0ex}}\text{V}\right)=16.0\phantom{\rule{0.2em}{0ex}}\mu \text{C,}\hfill \\ {Q}_{3}={C}_{3}{V}_{3}=\left(4.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}\right)\left(8.0\phantom{\rule{0.2em}{0ex}}\text{V}\right)=32.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}\text{.}\hfill \end{array}$

Significance As expected, the net charge on the parallel combination of ${C}_{2}$ and ${C}_{3}$ is ${Q}_{23}={Q}_{2}+{Q}_{3}=48.0\phantom{\rule{0.2em}{0ex}}\mu \text{C}\text{.}$

Summary

When several capacitors are connected in a series combination, the reciprocal of the equivalent capacitance is the sum of the reciprocals of the individual capacitances.
When several capacitors are connected in a parallel combination, the equivalent capacitance is the sum of the individual capacitances.
When a network of capacitors contains a combination of series and parallel connections, nosotros place the series and parallel networks, and compute their equivalent capacitances pace by step until the entire network becomes reduced to one equivalent capacitance.

Conceptual Questions

If you wish to store a large corporeality of charge in a capacitor bank, would you connect capacitors in series or in parallel? Explicate.

What is the maximum capacitance y'all can get by connecting three $1.0\text{-}\mu \text{F}$ capacitors? What is the minimum capacitance?

$3.0\phantom{\rule{0.2em}{0ex}}\mu \text{F},0.33\phantom{\rule{0.2em}{0ex}}\mu \text{F}$

Problems

A iv.00-pF is connected in series with an viii.00-pF capacitor and a 400-V potential difference is applied across the pair. (a) What is the charge on each capacitor? (b) What is the voltage across each capacitor?

a. 1.07 nC; b. 267 V, 133 V

Find the total capacitance of this combination of series and parallel capacitors shown below.

Figure shows capacitors of value 10 micro Farad and 2.5 micro Farad connected in parallel with each other. These are connected in series with a capacitor of value 0.3 micro Farad.

$0.29\phantom{\rule{0.2em}{0ex}}\mu \text{F}$

Suppose you demand a capacitor banking concern with a full capacitance of 0.750 F merely you have only one.50-mF capacitors at your disposal. What is the smallest number of capacitors you could connect together to attain your goal, and how would you connect them?

500 capacitors; connected in parallel

What total capacitances tin you lot brand by connecting a $5.00\text{-}\mu \text{F}$ and a $8.00\text{-}\mu \text{F}$ capacitor?

$3.08\phantom{\rule{0.2em}{0ex}}\mu \text{F}$ (series) and $13.0\phantom{\rule{0.2em}{0ex}}\mu \text{F}$ (parallel)

Find the equivalent capacitance of the combination of series and parallel capacitors shown below.

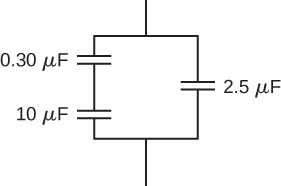
Figure shows capacitors of value 0.3 micro Farad and 10 micro Farad connected in series with each other. These are connected in parallel with a capacitor of value 2.5 micro Farad.

Find the net capacitance of the combination of series and parallel capacitors shown below.

$11.4\phantom{\rule{0.2em}{0ex}}\mu \text{F}$

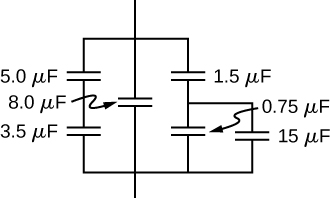
A 40-pF capacitor is charged to a potential difference of 500 V. Its terminals are then continued to those of an uncharged x-pF capacitor. Calculate: (a) the original charge on the 40-pF capacitor; (b) the charge on each capacitor after the connection is made; and (c) the potential difference across the plates of each capacitor after the connexion.

A $2.0\text{-}\mu \text{F}$ capacitor and a $4.0\text{-}\mu \text{F}$ capacitor are connected in series beyond a one.0-kV potential. The charged capacitors are then disconnected from the source and connected to each other with terminals of similar sign together. Notice the accuse on each capacitor and the voltage across each capacitor.

0.89 mC; 1.78 mC; 444 V

Glossary

parallel combination: components in a circuit arranged with one side of each component continued to one side of the excursion and the other sides of the components connected to the other side of the circuit

series combination: components in a circuit arranged in a row one afterward the other in a circuit

danielsvirinarlecou.blogspot.com

Source: https://opentextbc.ca/universityphysicsv2openstax/chapter/capacitors-in-series-and-in-parallel/

What Is the Equivalent Capacitance of the Circuit to the Right?

50 Capacitors in Serial and in Parallel

Learning Objectives

The Series Combination of Capacitors

The Parallel Combination of Capacitors

Summary

Conceptual Questions

Problems

Glossary

0 Response to "What Is the Equivalent Capacitance of the Circuit to the Right?"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel